VECTORES

                 ¿Qué es un Vector?

En fisica un vector (vector euclidiano o vector geométrico) es una magnitud fisica definida en un sistema de referencia que se caracteriza por tener modulo(o longitud) y una dirección.

¿Cómo de simbolizan los vectores?

Los vectores lo podemos simbolizar de dos formas:

_Gráficamente por segmentos

Agregar leyenda

_Analíticamente por letras con una flecha

Características de los vectores

_Tiene origen (Punto inicial)

_Tienen extremo (Punto final)

_Tienen sentido (Positivo o negativo)

_Tienen dirección

_Tienen modulo

Suma de Vectores

Los vectores se pueden sumar usando dos métodos :

Métodos gráficos

_Metodo del Triangulo

En este método, los vectores se deben trasladar de tal forma que la "cabeza" del uno se conecte con la "cola" del otro. El vector resultante se representa por la "flecha" que une la "cola" que queda libre con la "cabeza" que también está libre (es decir se cierra un triángulo).

_Método del Paralelogramo

Primero se dibujan ambos vectores (a y b) a escala, con el punto de aplicación común.Seguidamente, se completa un paralelogramo, dibujando dos segmentos paralelos a ellos. El vector suma resultante (a+b) será la diagonal del paralelogramo con origen común a los dos vectores originales.

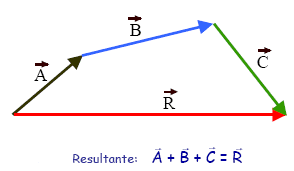
_Método del Poligono

El método consiste en colocar en secuencia los vectores manteniendo su magnitud, a escala, dirección y sentido; es decir, se coloca un vector a partir de la punta flecha del anterior. El vector resultante esta dado por el segmento de recta que une el origen o la cola del primer vector y la punta flecha del último vector.

Suma de vectores por métodos analíticos.-son dos los métodos.

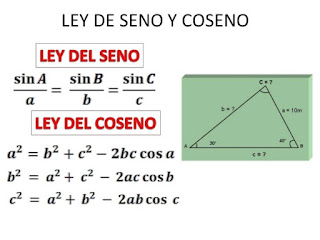
1.- Método de la ley de cosenos y senos: Esto método solo sirven para sumar dos vectores.

·         LEY DE COSENOS. Se establece considerando los módulos de los vectores que se suman y el ángulo que forman.

·         LEY DE SENOS. Se establece considerando el triángulo de vectores que se suman y su resultante, además de los ángulos interiores que se forman.

     2.-Método de componentes: Para usar el método de componentes los módulos de los vectores deben expresarlos vectorial mente en sus componentes rectangulares.

     Componente de un vector, es la proyección del vector sobre una línea de referencia (pueden ser los ejes coordenadas), así:

                          Componentes vectoriales en dos dimensiones:

                        Componentes vectoriales en tres dimensiones: